For those of you who are unfamiliar with the point count system in chess, it works like this: Every piece has a number of points. Pawns are 1 point. Knights and bishops are 3 points each. Rooks are 5 points. The queen is 9. We don’t assign a number of points to the king. Why? Because the king cannot be traded. (With the exception of kindergarten-level chess, the game ends in checkmate before a player is able to snatch up their opponent’s king and place their own piece on its square.) The whole reason for the point count system is to serve as a guide for when and how we should trade our pieces for our opponent’s pieces. According to this system, it’s OK to trade knight for a bishop. That’s an equal trade. It’s usually not a good idea to trade a rook for a bishop. You would lose 2 points.
I say ‘usually’ because the values of the pieces varies in relation to the positions that they occupy. Imagine you a General commanding an army. Your army is fighting a battle on a flat grassy plain. A soldier who is a proficient rock climber is of no special use to you. However, if you are fighting in the mountains, the same soldier quickly becomes very useful. Each piece in chess, like rock climbers, sprinters, and scuba divers operates best when in positions that suit them. Determining when a piece is in its element is complicated, but let’s simplify it. The primary source of value for a piece is its mobility. The more squares a piece can travel to, the more opportunities it has to engage with the enemy, both offensively and defensively. Rooks have more mobility in open positions because they can fly all the way across the board. Knights can’t do this, so knight might be stronger, relatively speaking more closed positions.
We shouldn’t exclusively look at the number of squares a piece can move to at a given moment in a game. We should also think about the piece’s potential to controls square in the future. This is especially important for Rooks. Rooks are long range, open-space loving fellows who generally preform well in endgames. In the opening, rooks tend to look pretty pitiful. They are often boxed in behind their own pieces and limited in their movement to one or two squares. But don’t be so fast to trade your rook for a knight on move 8! Something funny happens in chess. Pieces come off the board, they don’t go back on. As chess games progress, the board tends to declutter. And guess who comes to life? That’s right, our favorite flying castle. It’s the potential for the rook to become a later-stage beast that give it value long before the bull is released from it’s pin.
But shouldn’t this idea of a ‘promising future’ also apply to the the bishops? Aren’t bishops the same as rooks, essentially? Both both pieces travel in long, straight lines. In fact, what is a bishop but a rook who has been rotated 45 degrees?
Let’s look a little more closely.
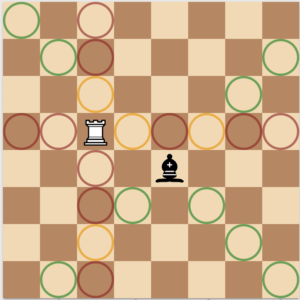
Here we have placed a rook and a bishop in the roughly the middle of the board.
A quick count reveals that there are 13 squares that the bishop can move to (green and yellow). The rook can move to 14 squares. Hmmm.
Where does this extra square come from? Shouldn’t it be the same? It might be a little confusing, but we will clarify this soon. Regardless, 14 is not significantly greater than 13. Certainly not enough to explain why the rook is worth almost twice what a bishop is.
Let’s look at another example:
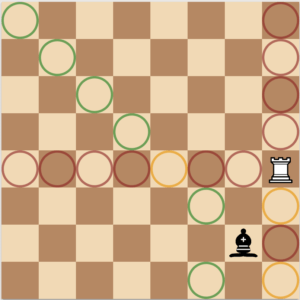
In this example the rook and the bishop have been moved further from the center. Let’s count the number of squares that they can travel to again.
Rook: 14, Bishop 9.
Wait, What! Why did the bishop get so wimpy on us? Shouldn’t it be the same distance from side to side to matter where you are? Not if you are on a diagonal. Diagonals on the chess board vary in length, while ranks and files remain the same. On an open board, a rook on any square will have a greater range of movement than the best placed bishop. The closer the bishop gets to the side of the board, the more pronounced this difference is. But this is only part of the story. The Rook has twice as many potential squares as the bishop. The Rook can visit every square on the chess board, while the bishop, confined to a certain color of square, can only visit half of them. Talk about limited potential!
Let’s look at endgame position that illustrates various ways in which the rook is able to flex his might over the bishop.
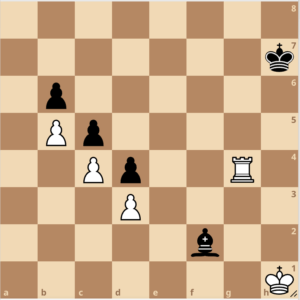
In this position, the only real difference between the two sides is that White has a rook and Black has a bishop. And yet, White is completely winning. White is so winning, he can choice between different winning plans. Let’s notice some differences between the bishop and the rook.
The White pawns are on light squares, therefore the dark-squared bishop can never attack them. The best that he can do is defend his own pawns. Were all the pawns on the opposite colored squares, the reverse problem would be true- Black would be able to attack the opponents pawns but unable to defend his own. Combine this observation with another: The rook can build an impassable barrier for a king. The bishop has no such power. Look at the poor Black king on h7. He can is stuck on the h-file because of the rook on the g-file. Is the Black bishop trapping the white king in the corner by making a barrier across the e1-h4 diagonal? Me thinks not! White can lock the Black king out of the game, preventing him from getting close to the pawns. The bishop can not touch the pawns- they are on the wrong color. And lastly, the pawns themselves can not move. This should be enough to suggest that White can’t lose.
How does white win?
This is your job. Demonstrate a white for White. Write down your variations. No cheating and playing good moves for White and bad ones for Black! Show Black’s stiffest resistance! Once you show that a white pawn will queen before a black pawn can, you may end your variation.
All this may lead you to believe that a rook should be worth 4 bishops. In the next installment, we will look at positions where the bishop has the upper hand!



